By Augie Bennett
Fractions don’t have to be tricky—whether you’re adding, subtracting, multiplying, or dividing, we’ll break it down with simple steps and real-life examples. Master fractions once and for all with this easy guide!
What are fractions?
Fractions are used to represent parts of a whole, and are written in the form
A
B, where B is the total number of parts (called the denominator), and A is the number of parts you have (called the numerator).
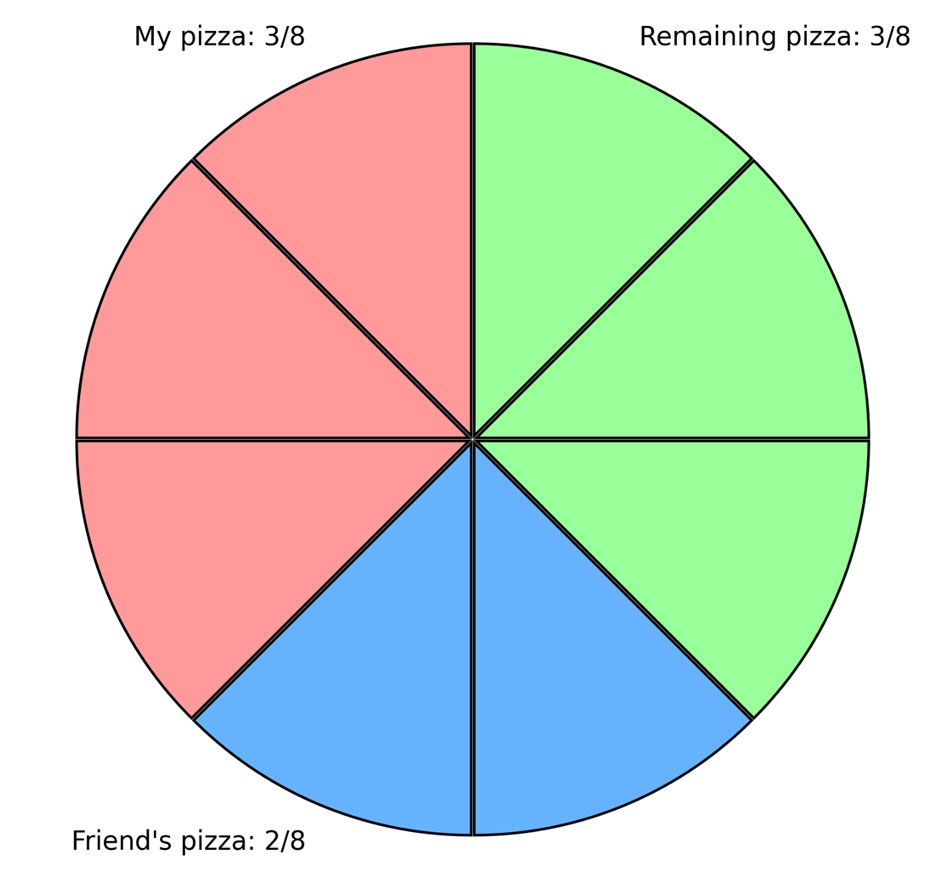
In the following examples, we will use a pizza that is cut into 8 equal pieces. In this case, each slice of the pizza represents
1
8 of the whole pizza. In the below image, I have
3
8 slices of pizza, and my friend has
2
8 slices of pizza.
Addition of Fractions
Adding and subtracting fractions with the same denominator is straightforward: you just add the numbers on the top! For example, this pizza is cut into 8 pieces, so I can add the
3
8 of the pizza that I eat with the
2
8 of the pizza that my friend eats. Together, my friend and I eat
5
8 of the pizza:
What is 3
8 + 2
8?
Me: 3
8
My friend: 2
8
Total consumed together: 3
8 + 2
8 = 5
8
Subtraction of Fractions
Just like addition, subtracting fractions with the same denominator is easy! You subtract the top numbers (the numerator) while keeping the bottom numbers (the denominator) the same.
For example, if I ate
3
8 of the pizza and my friend ate
2
8, we can figure out how much pizza remains by subtracting the amount we ate from the whole pizza.
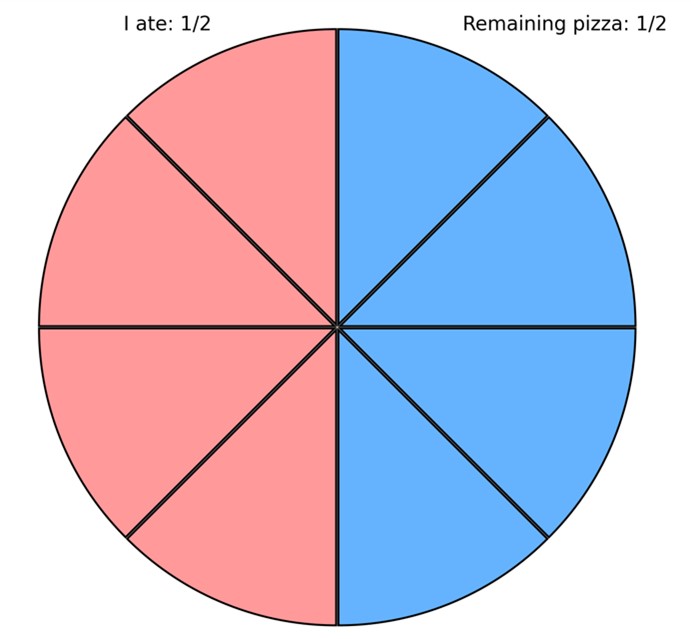
What is 8
8 – 5
8?
Total pizza: 8
8 (the entire pizza)
Pizza eaten: 5
8 (my 3
8 + my friend’s 2
8, from the addition example)
Remaining pizza: 8
8 – 5
8 = 3
8
So, 3
8 of the pizza is left.
Multiplication of Fractions
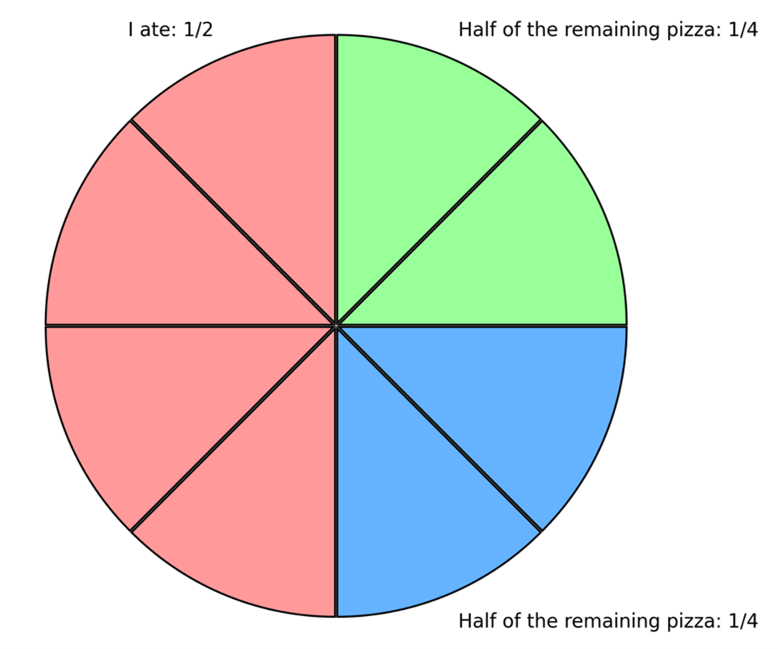
To multiply fractions, simply multiply the numerators and then multiply the denominators. Let’s say I eat
1
2
of a pizza, and my friend and I want to split the remaining amount evenly. How much of the total pizza does my friend get to eat?
What is 1
2 multiplied by 1
2?
I ate: 1
2
Pizza Remaining: 1
2
My friend’s share of the remaining pizza:
1
2
*
1
2
=
(1 * 1)
(2 * 2)
=
1
4
My share of the remaining pizza:
1
2
*
1
2
=
(1 * 1)
(2 * 2)
=
1
4
So, 1
2 of 1
2 of the pizza is 1
4 of the pizza!
Division of Fractions
Dividing fractions may seem tricky at first, but there’s a simple trick to make it easy: remember to flip the second fraction (the one you’re dividing by) and then multiply the two fractions together. Division is the opposite of multiplication: can you use the above figure to solve the following problem?
What is 1
2 divided by 1
4?
For example, if I have
1
2
of a pizza and I want to divide it into portions that are
1
4
of the pizza each, I divide
1
2
by
1
4:
1
2 ÷
1
4 =
1
2 *
4
1 =
(1 * 4)
(2 * 1)
=
4
2 = 2
This means my
1
2
pizza contains 2 portions of
1
4
each!
Addition and Subtraction with Different Denominators
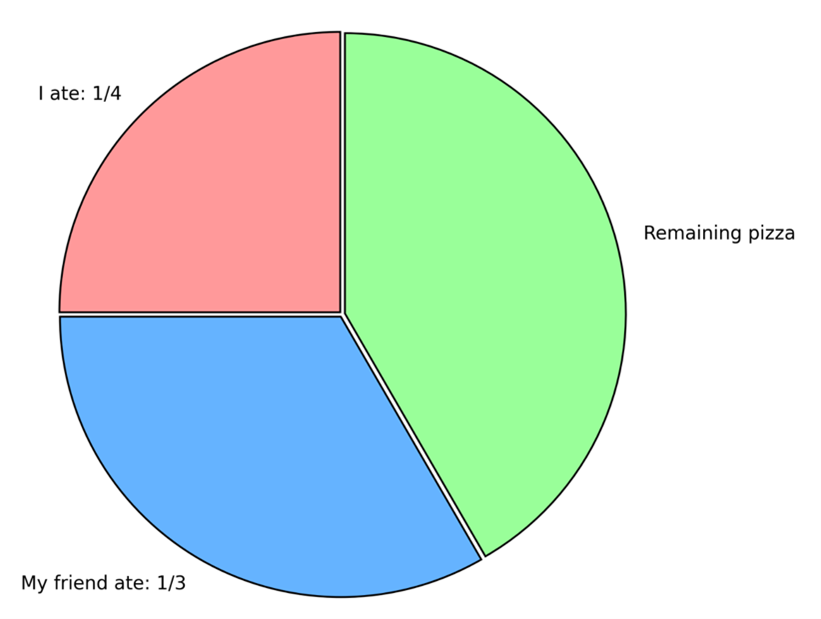
When adding or subtracting fractions with different denominators, we need to find a common denominator first. Let’s say I eat
1
3
of a pizza, and my friend eats
1
4.
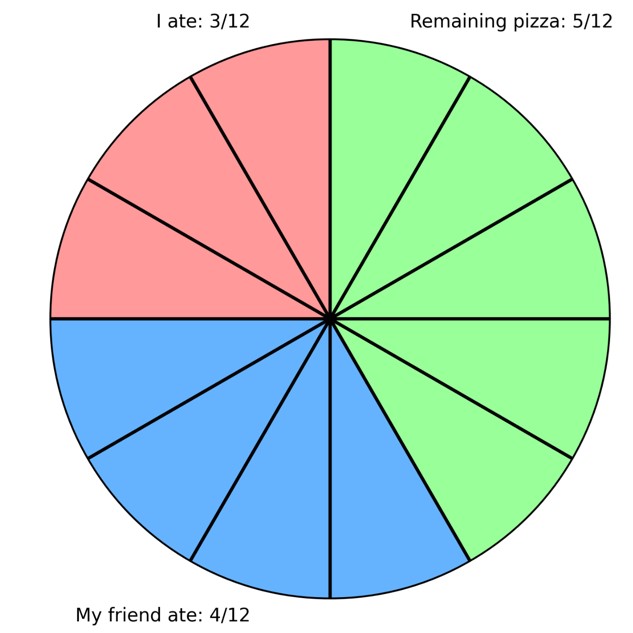
To figure out how much we eat together, we need to find the least common denominator (LCD) of 3 and 4. The LCD of 3 and 4 is 12, so we convert the fractions:
1
3 =
4
12
1
4 =
3
12
Now that the fractions have the same denominator, we can add:
4
12 +
3
12 =
7
12
So, together we have
7
12
of the pizza.
Subtraction works the same way—just subtract the numerators after finding a common denominator. Can you find how much pizza is left after I eat
1
3
and my friend eats
1
4?
In Conclusion
Fractions allow us to break things down into smaller, manageable parts. Whether you’re adding, subtracting, multiplying, or dividing, understanding fractions helps you navigate the math behind everyday situations. With the pizza example in mind, you can now confidently tackle any fraction problem!